题16
题目
(I) 比较
(II) 记
分析
第一问比大小应该是定积分的保号性,关键在于比较
但是第一问我用的是定积分的中值定理,第二问证明数列收敛或者说证明数列有极限,单调有界准则是百试百灵的通法
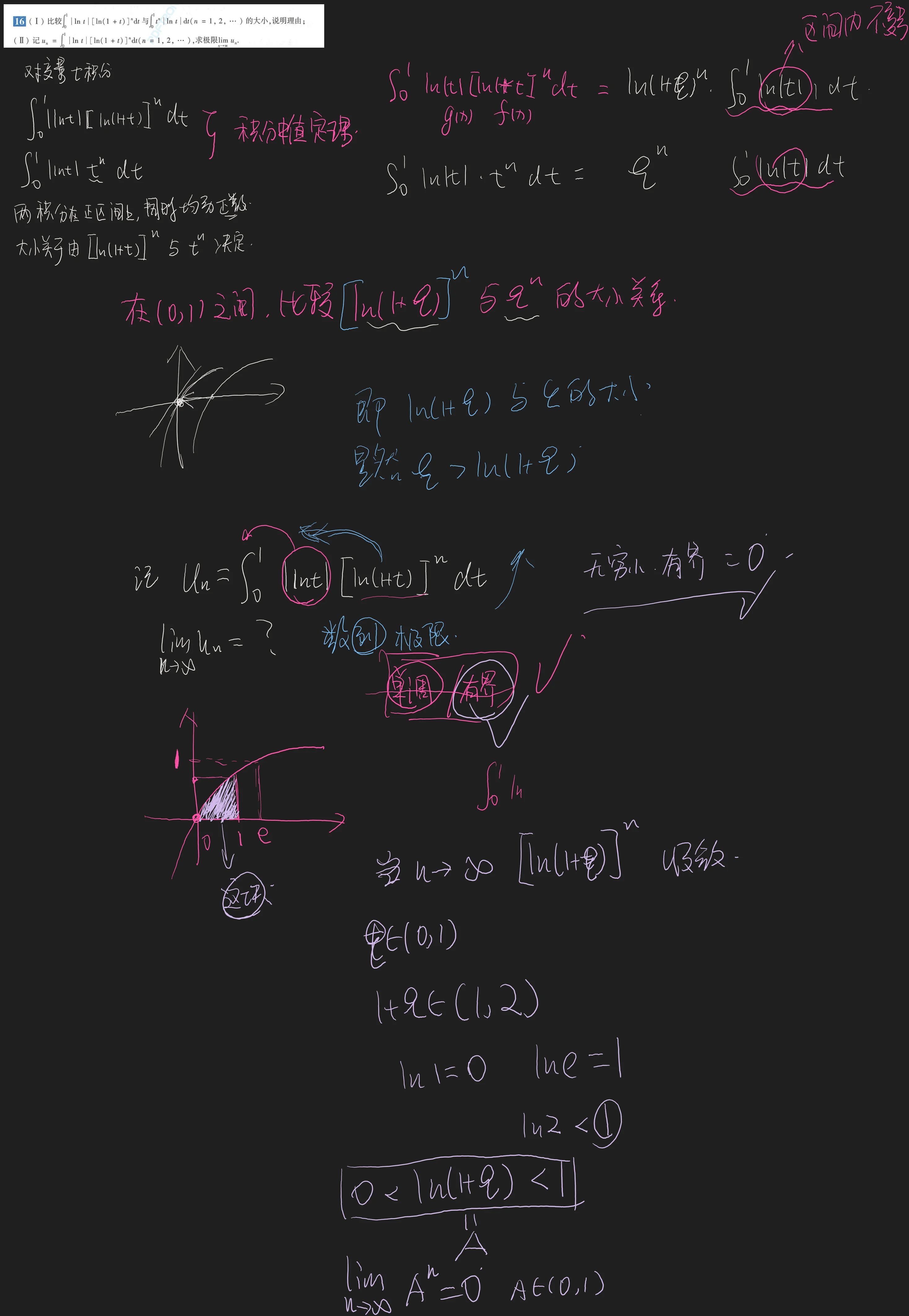
解
(解) (I) 在
考虑
当
因此,当
(II) (法一) 由第(I) 问知,
因此,
由夹逼准则知,
(法二) 由第( I ) 问知,
又因为
由夹逼准则知,
(法三) 由于
计算
从而
因为
注 ① 在解第 ( II ) 问时,下面的做法是不严谨的.
由第 (I) 问可得
因此,
由夹逼准则知,
这是因为,对
② 在用夹逼准则求极限值时,一般要对原数列的界做估计. 第 (I) 问提供了一种估计, 法三没有利用第 ( I ) 问的结论, 而是提供了另一种估计方法, 都是可行的. 但是要注意, 使用法三时,一定要说明反常积分
③ 第 ( II ) 问中,“