题7

题7

题目

[!question]+
(7) 设 均为 2 阶方阵, 分别为 的伴随矩阵. 若 ,则分块矩阵 的伴随矩阵为 ( )
(A) .
(B) .
(C) .
(D) .

分析

[!NOTE]+
拉普拉斯展开式-分块矩阵算的是行列式，不是逆，也不是伴随矩阵，和题2.9、题8还有例3.17都是一个考点，通法是用矩阵方程

解

[!done]-

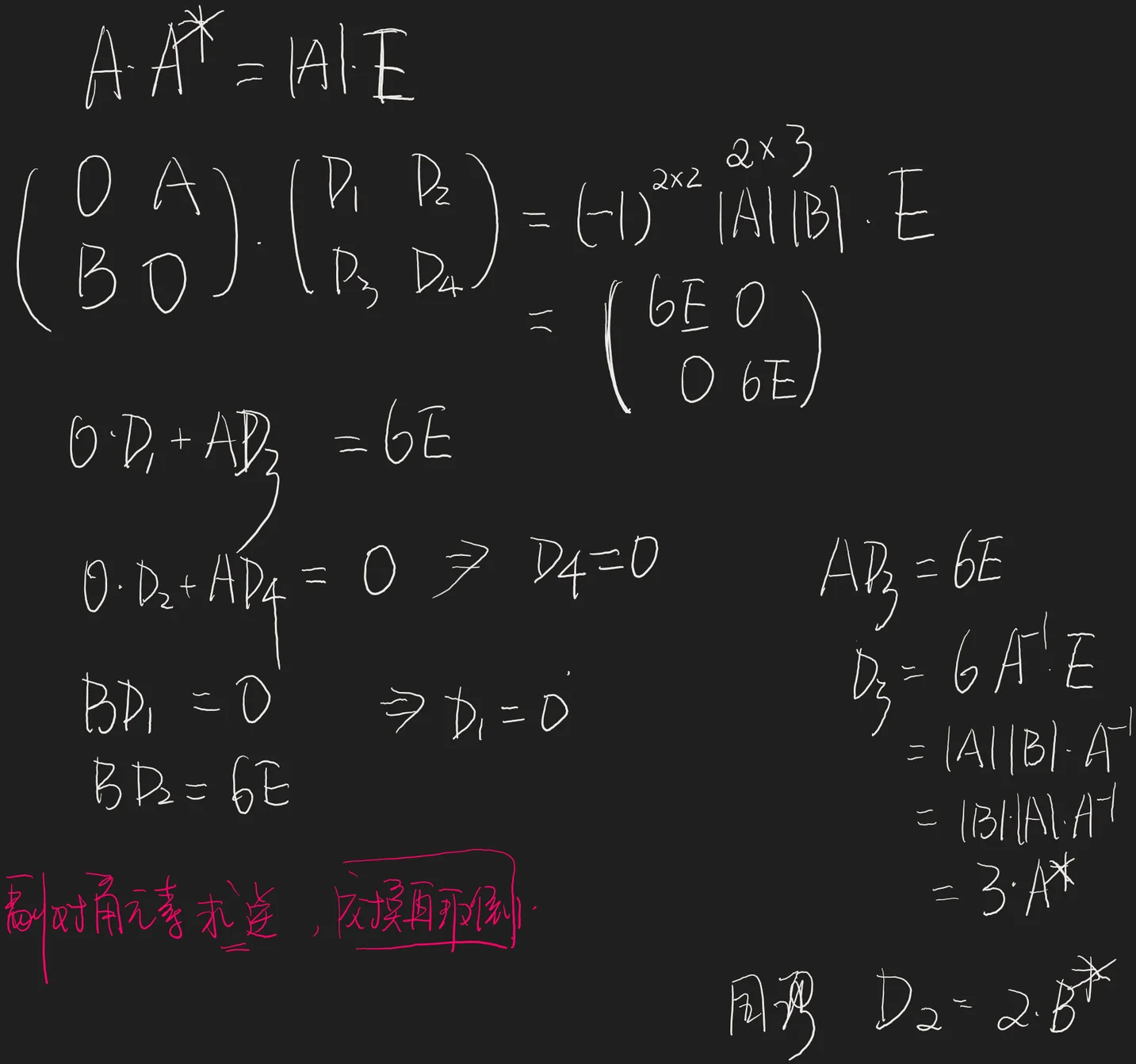
方阵与它的伴随矩阵的关系 .

可逆矩阵与它的伴随矩阵的关系 若矩阵 可逆,则 .

对本题而言,可设 的逆矩阵或伴随矩阵为 ,通过解矩阵方程求解.

解 (法一) 先求 .

记 为 4 阶矩阵, 位于它的第 1,2 行和第 3,4 列,可按照以下步骤把 变为

. 把 的第 3 列与第 1 列对换,第 4 列与第 2 列对换.

因此,

可逆.

由可逆矩阵与其伴随矩阵的关系可知,

不妨设 ,则

由于 均为可逆矩阵,故由 可知, ; 由

得, .

因此,

应选 B.

(法二) 不妨设 .

由法一知, ,故

从而,

由此可推出, .

因此, . 应选 B.

(法三) 特殊值法.

取 满足 ,则 . 因此,

应选 B.

(注) 法三中用到了分块矩阵的求逆公式 对任意 阶可逆矩阵 阶可逆矩阵 , 有