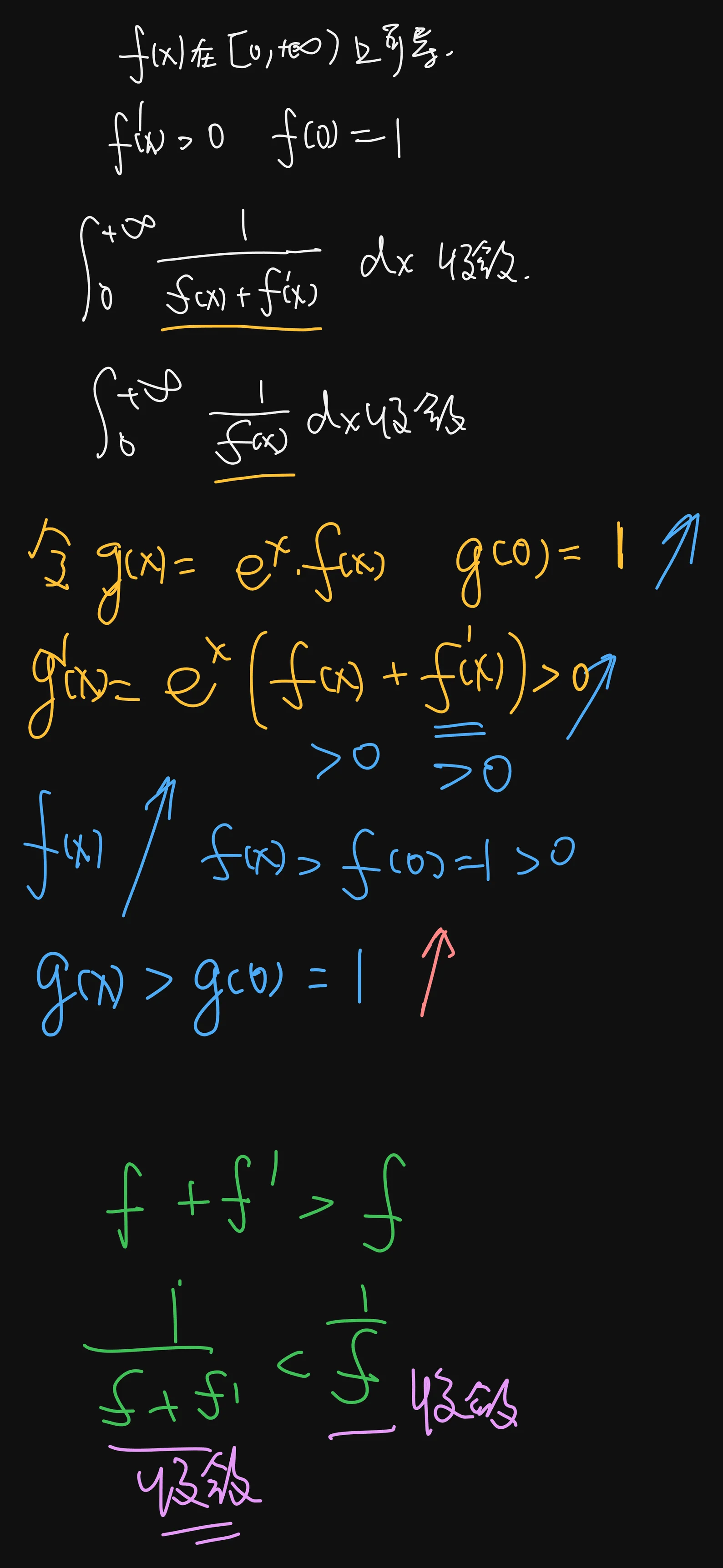例8.19
题目
Q:P207 设函数
(A) 充要条件
(B) 充分非必要条件
(C) 必要非充分条件
(D) 既非充分也非必要条件
分析
A:邂逅遗憾认为是好题,用等价无穷大的想法,特使是针对
两个东西互相判断是否收敛,用比较判别法-无穷区间上反常积分的思维来说,除了去做比,就是这个单调有界准则,和数列一样,去作差看看
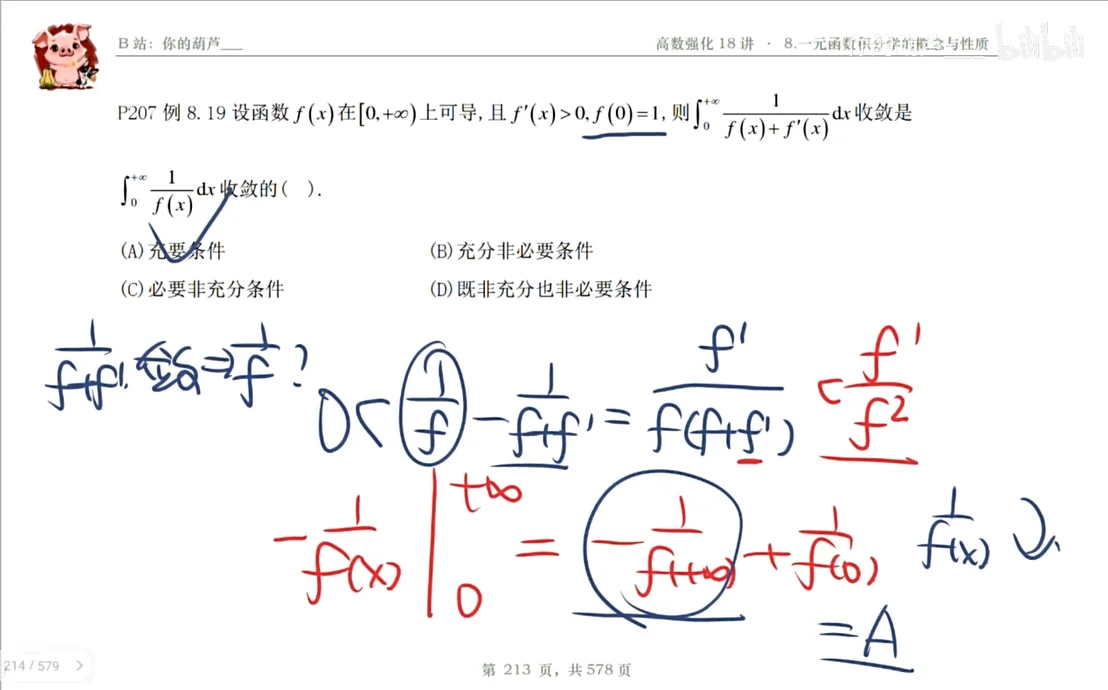
解
【解】应选(A).
依题设, 有
由于
又
故
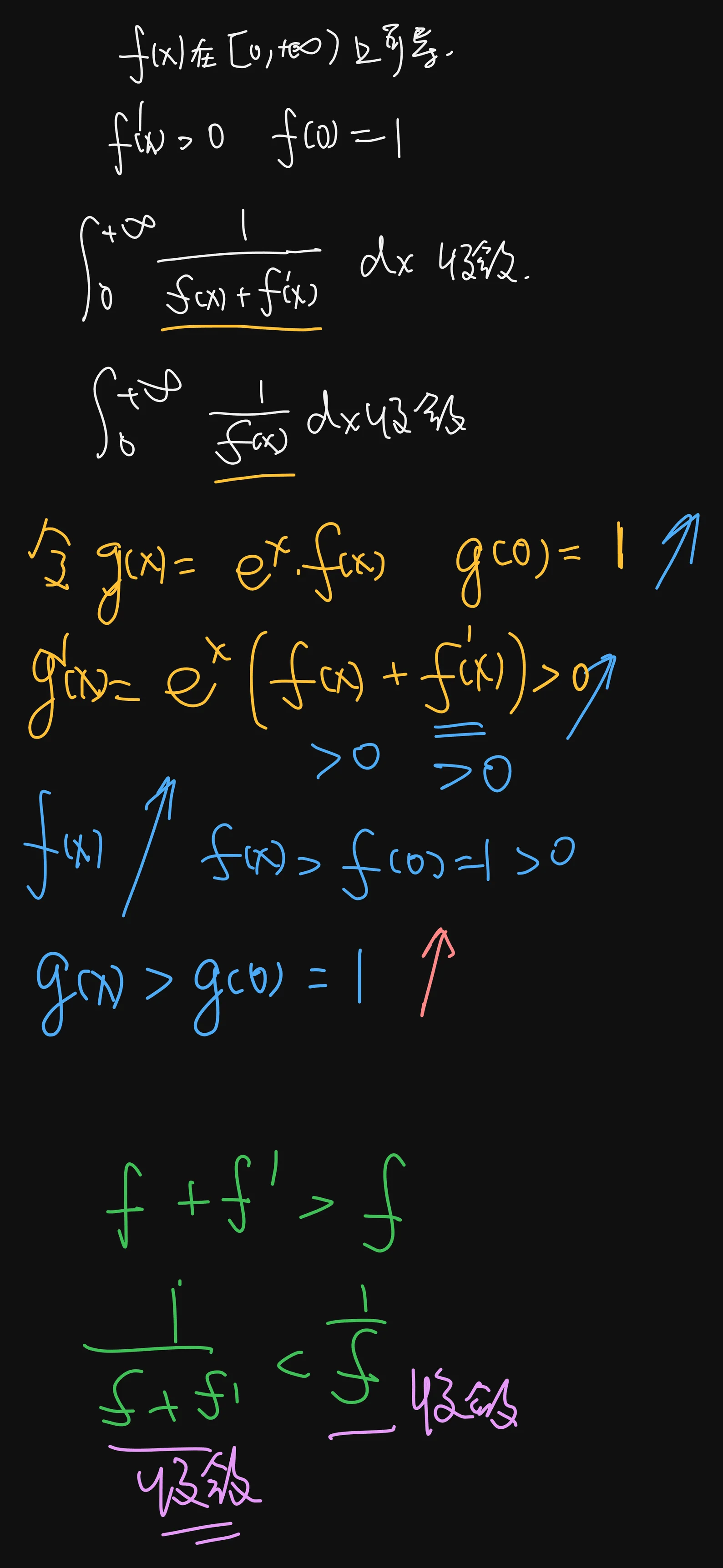
Q:P207 设函数
(A) 充要条件
(B) 充分非必要条件
(C) 必要非充分条件
(D) 既非充分也非必要条件
A:邂逅遗憾认为是好题,用等价无穷大的想法,特使是针对
两个东西互相判断是否收敛,用比较判别法-无穷区间上反常积分的思维来说,除了去做比,就是这个单调有界准则,和数列一样,去作差看看

【解】应选(A).
依题设, 有
由于
又
故