例6.9
题目
P141 设函数
内取得最小值, 证明:
(1) 存在
(2) 存在
分析
二阶可导,一阶必然是连续的
注意这里的开区间最值,说明这个最值点,一定是极值点,而不是在区间内单调然后在端点,往往这么隐藏起来的点是此地无银三百两,是关键
解
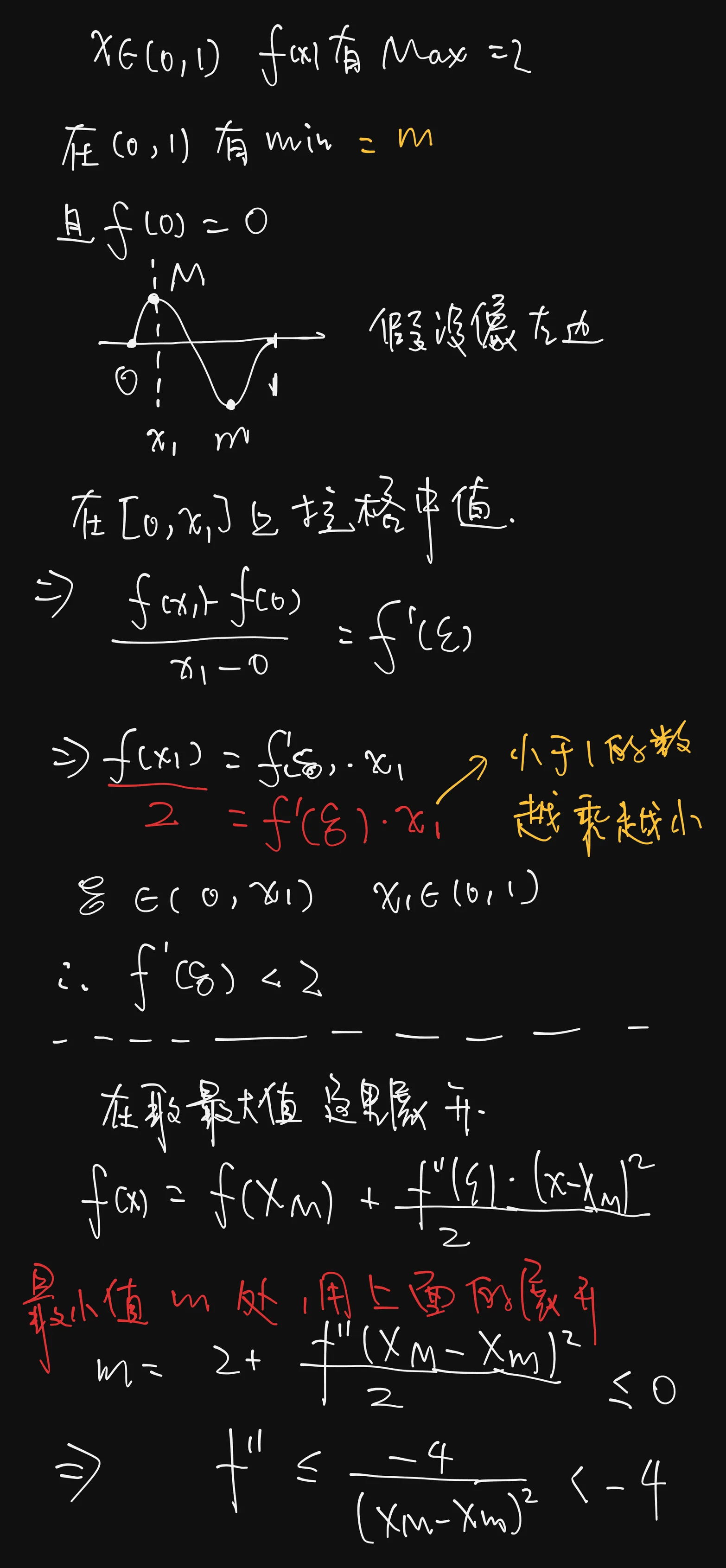
在
且
在
在
带入
Jun 19, 20252 min read
P141 设函数
内取得最小值, 证明:
(1) 存在
(2) 存在
二阶可导,一阶必然是连续的
注意这里的开区间最值,说明这个最值点,一定是极值点,而不是在区间内单调然后在端点,往往这么隐藏起来的点是此地无银三百两,是关键
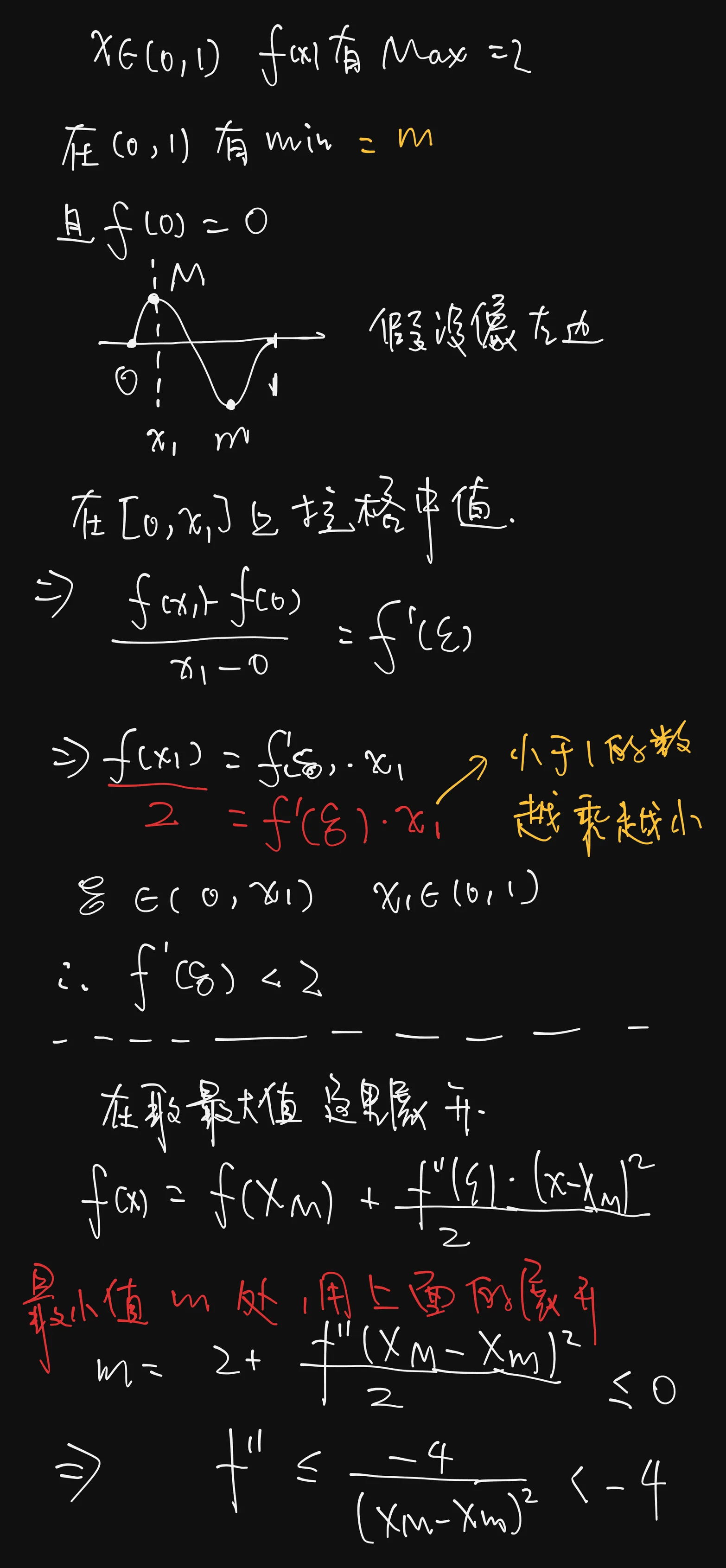
在
且
在
在
带入