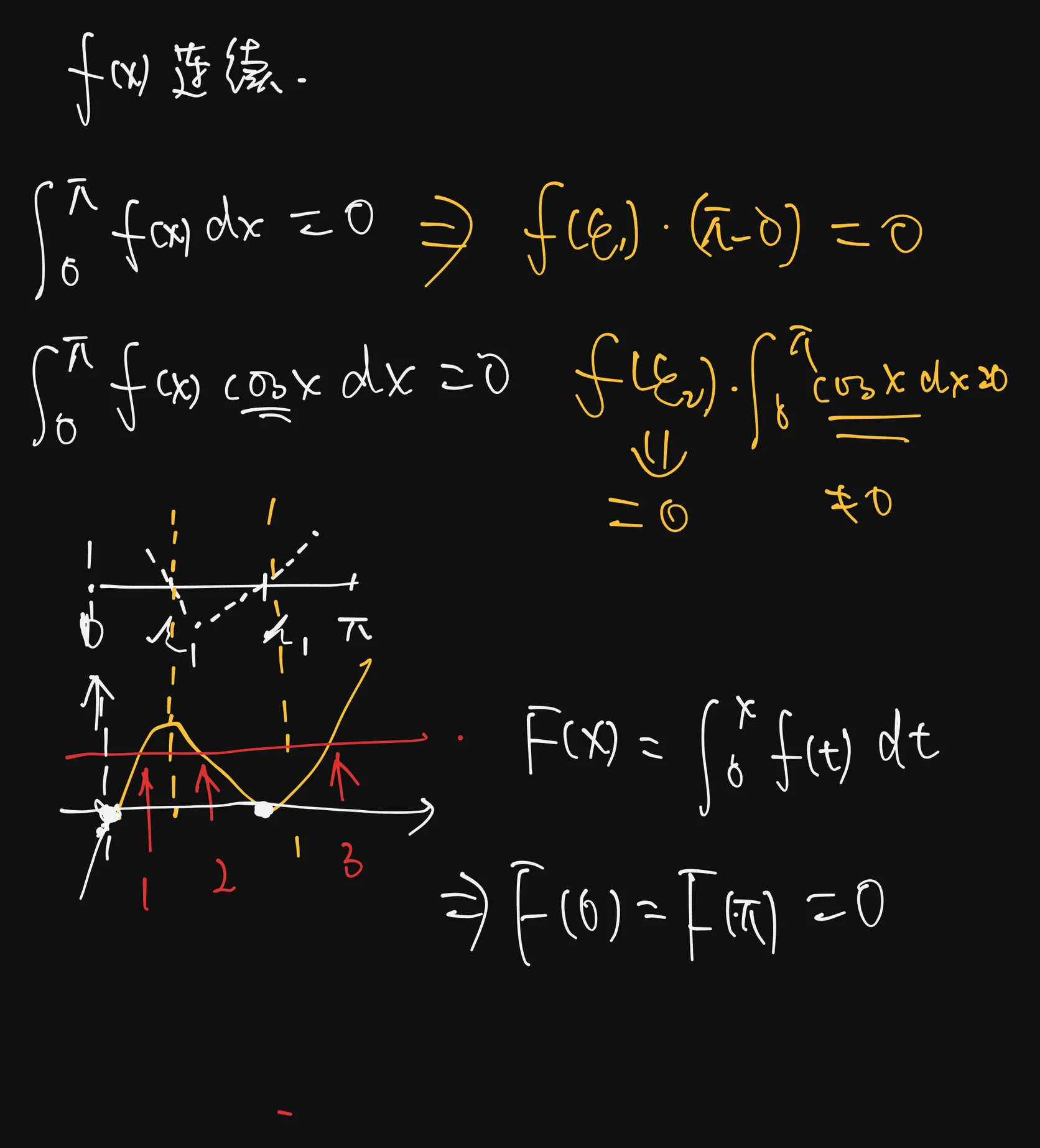例6.7
题目
Q:P140 设函数 在 上连续,且 .
证明: 在 内至少存在两个不同的点 ,使得 .
分析
A:可以考虑用两次定积分的中值定理,但是没办法保证两次的是两个不同的
这种题目都是用变限、变参
还有是把原函数提出来
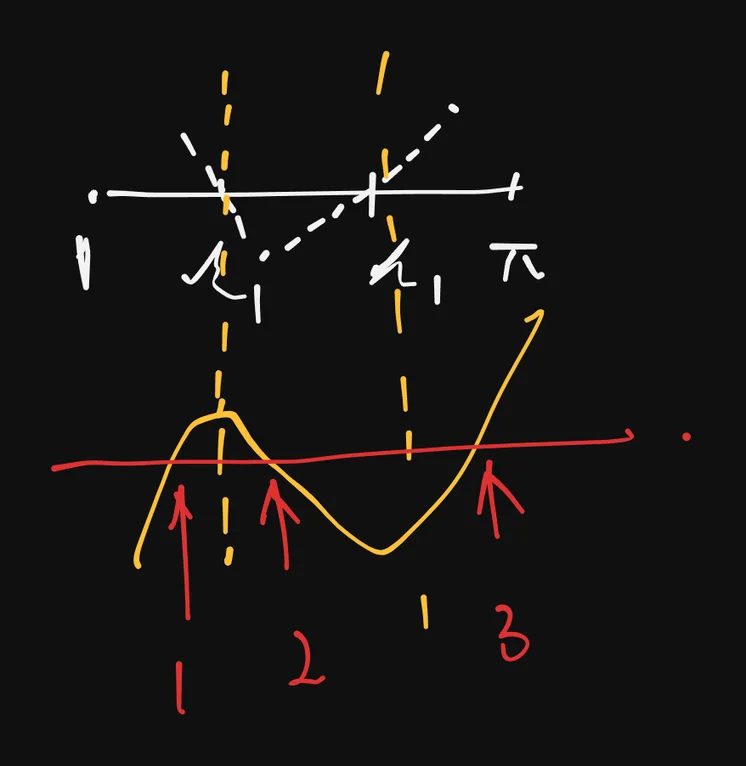
这里把积出来的视作是的话,由题目,就有两个导数为0的点,那么就可以画出来单调性的图,就有这个三个原函数相同的点
解

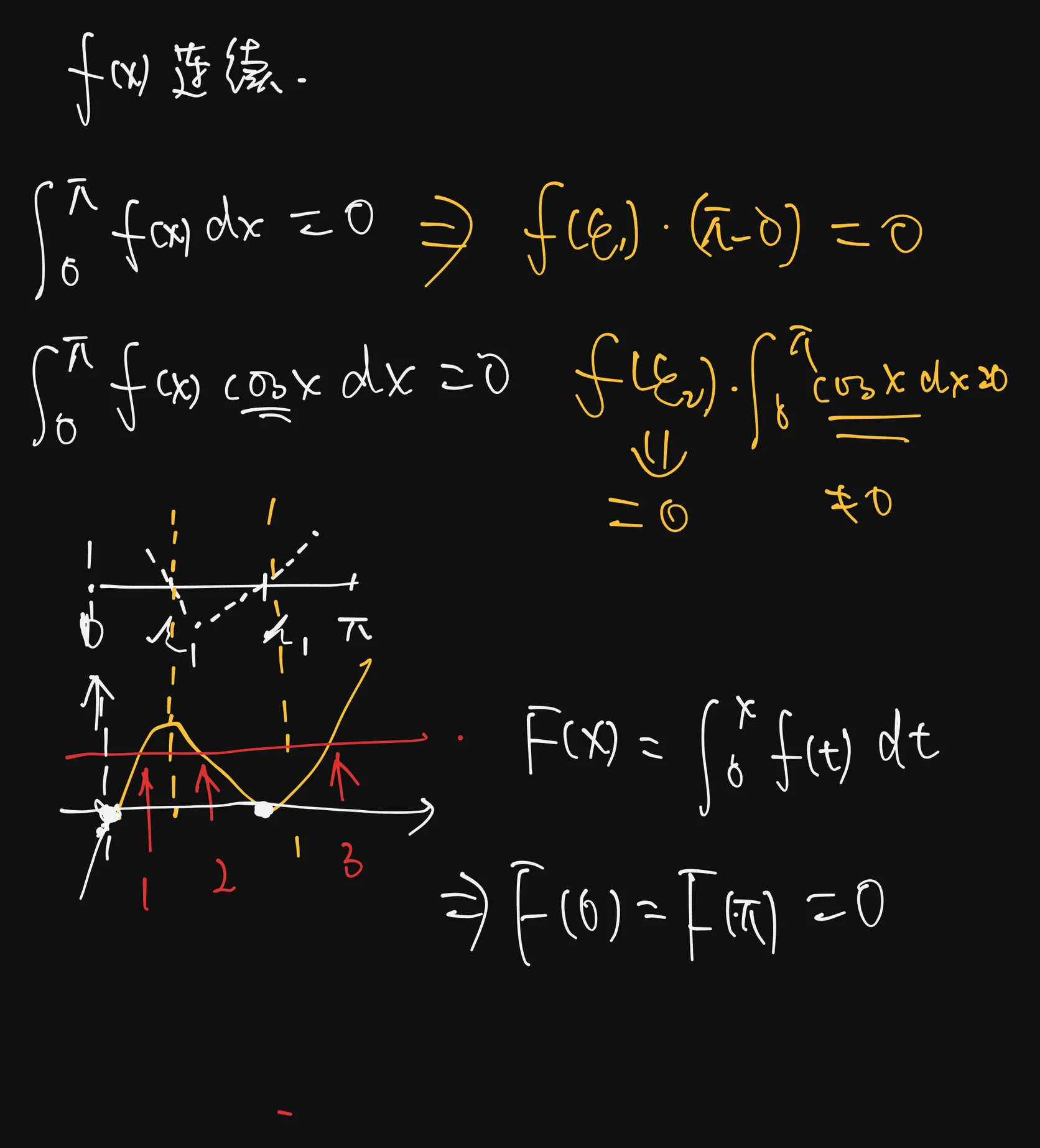
【证】令 ,则有 . 又因为
所以存在 ,使得 . 又当 时, . 故 .
由上证得 .
再对 在区间 上分别应用罗尔定理,知至少存在两点 ,使得 ,即 .