例6.10
题目
P142 设函数
证明:
(1) 存在
(2) 存在
(3) 存在
分析
第1问是例6.1里做过的,只不过它让证明
证明
- 一种是,构造一个
这种结构,然后求导得到 - 另一种是去泰勒展开里面找
这一项 - 第三种其实也算是第一种,比如题目这里的第三问,也直接差了一辈,只有
和 ,可以手动补项,补一个
(1) 由例 6.1 知,存在,使得 .
(2) 令,则函数 在 上一阶可导,且
所以存在
令
(3) 由
解
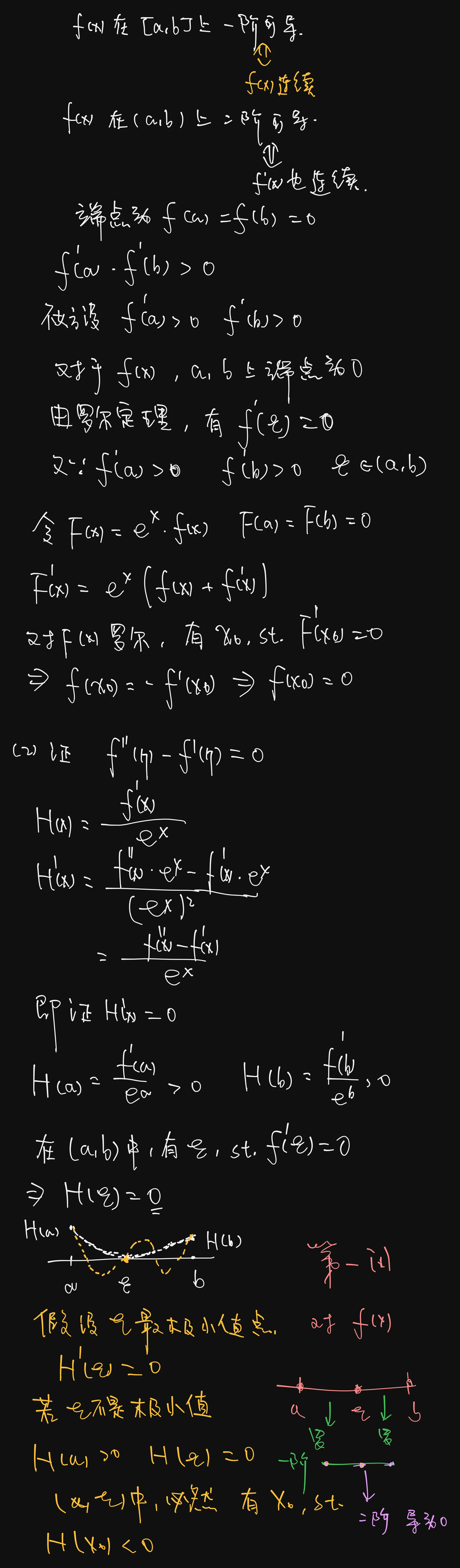
本题的难点在于证明
重点是第三问怎么用费马定理,第三问可以构造两种
一种是
另一种是
无论哪一种都可以用费马定理,主要的关键在于知道端点

构造函数
由于
- 当
时,根据 可知,图像在 点上升,在 点也上升,所以在 上存在最小值,即 。 - 当
时,根据 可知,图像在 点下降,在 点也下降,所以在 上存在最大值,即 。
所以与 同号。
又因为,且 ,所以 与 异号。
根据零点定理,在和 上分别存在一点使得 ,设为 ,则在 上存在一点使得 ,即存在 ,使得 。