例13.55

例13.55

题目

Q:P339 设函数在平面区域内连续,则以下四个命题:
①函数在其偏导数不存在的点也可能取到极值;
②若函数在内存在唯一驻点,则在内至多有 1 个极值点;
③若函数在内有 2 个极值点,则其中之一必为极大值点,另一个必是极小值点;
④ 在驻点处,若,则不是极值点.
正确命题的个数为( ).
(A) 1
(B) 2
(C) 3
(D) 4

分析

A:无约束极值的判断条件，要我们举出反例来，最好用的方法是，把一元的函数当做是多元的函数，一元函数是多元的子集，如果举的一元函数不满足题目叙述的性质，显然错误。如果说一元的特殊的函数怎么举，大概的方向是，振荡间断点的，还有这个绝对值的，或者是让分母为0没有定义的函数，这么几个方向来考虑

解

1是对的，234是错的


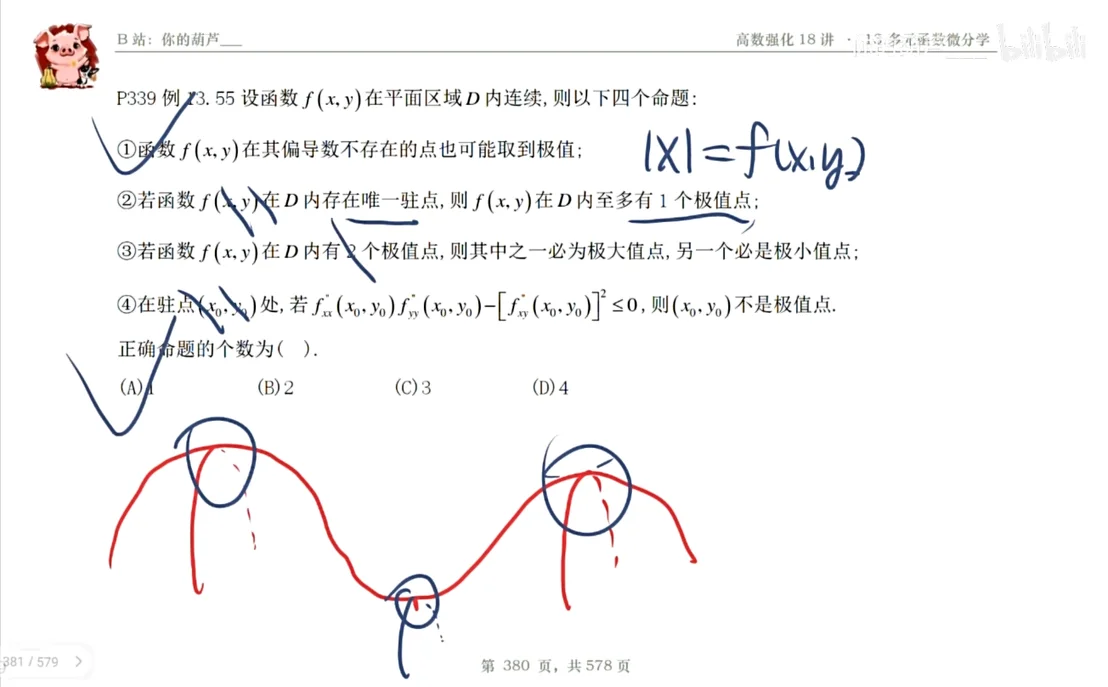
【解】应选(A)
①正确,例如函数 在原点 处取得极值
②错误, 因为偏导数不存在的点也可能是极值点
③错误,例如函数 的两个极值点均是极小值点 (见例 13.50)
④错误,例如函数 在原点 处取得极值