例3.5
题目
Q:P90 设函数
① 当
② 当
③ 当
④ 当
真命题的个数为 ( ) .
(A) 1 (B) 2 (C) 3 (D) 4
分析
A:对于有定义的理解,有定义,有极限,和函数值是三码事,有定义不代表连续
同时,这还是2020年数一的真题,也就是题5
这是极限的运算法则里面的那两个分式的结论
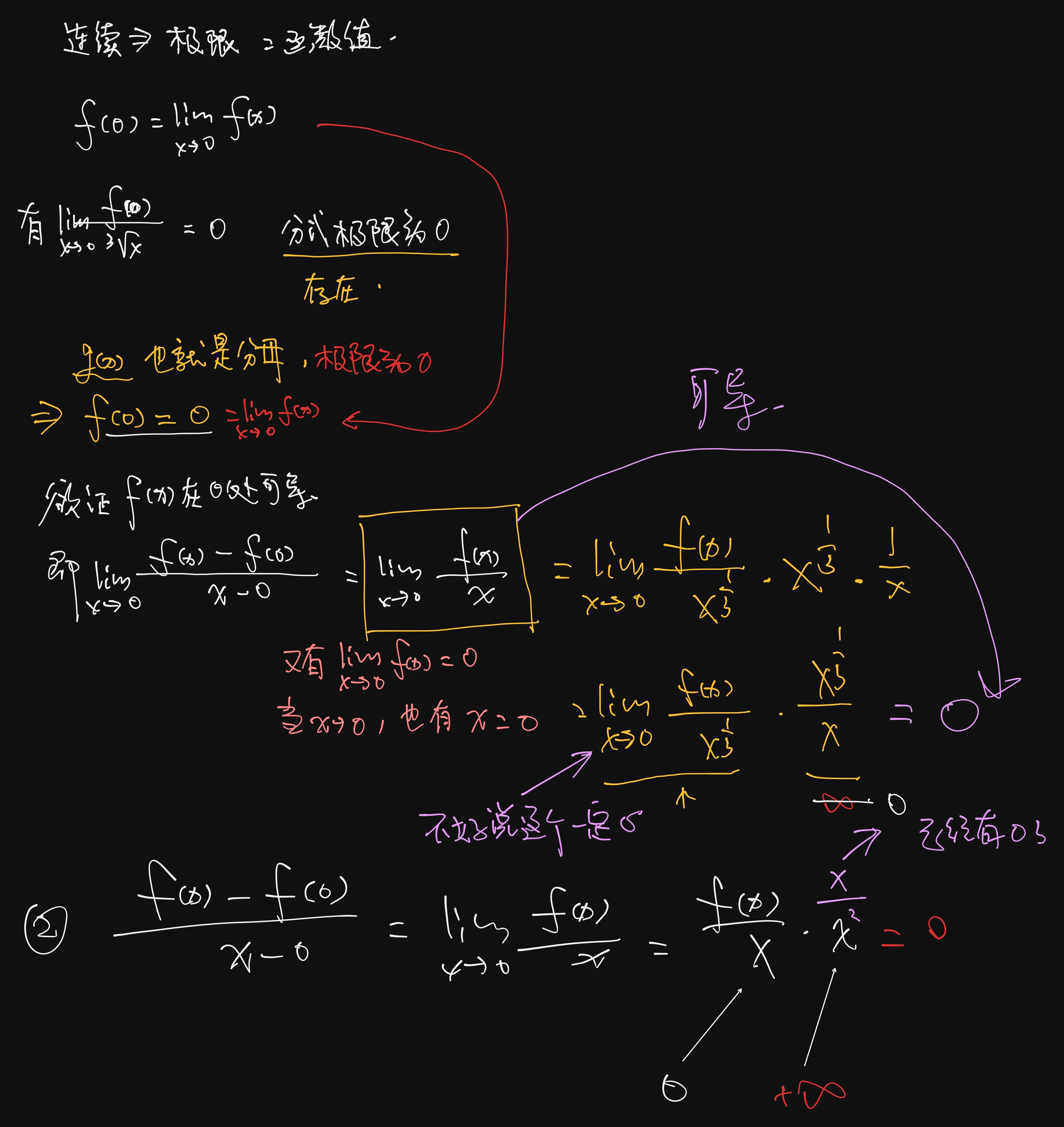
解
【解】应选(A).
①因为
因为
例如,取
②与①类似,可知
因为
③,④因为题目并没有给出条件
综上, 只有②正确.
Q:P90 设函数
① 当
② 当
③ 当
④ 当
真命题的个数为 ( ) .
(A) 1 (B) 2 (C) 3 (D) 4
A:对于有定义的理解,有定义,有极限,和函数值是三码事,有定义不代表连续
同时,这还是2020年数一的真题,也就是题5
这是极限的运算法则里面的那两个分式的结论

【解】应选(A).
①因为
因为
例如,取
②与①类似,可知
因为
③,④因为题目并没有给出条件
综上, 只有②正确.