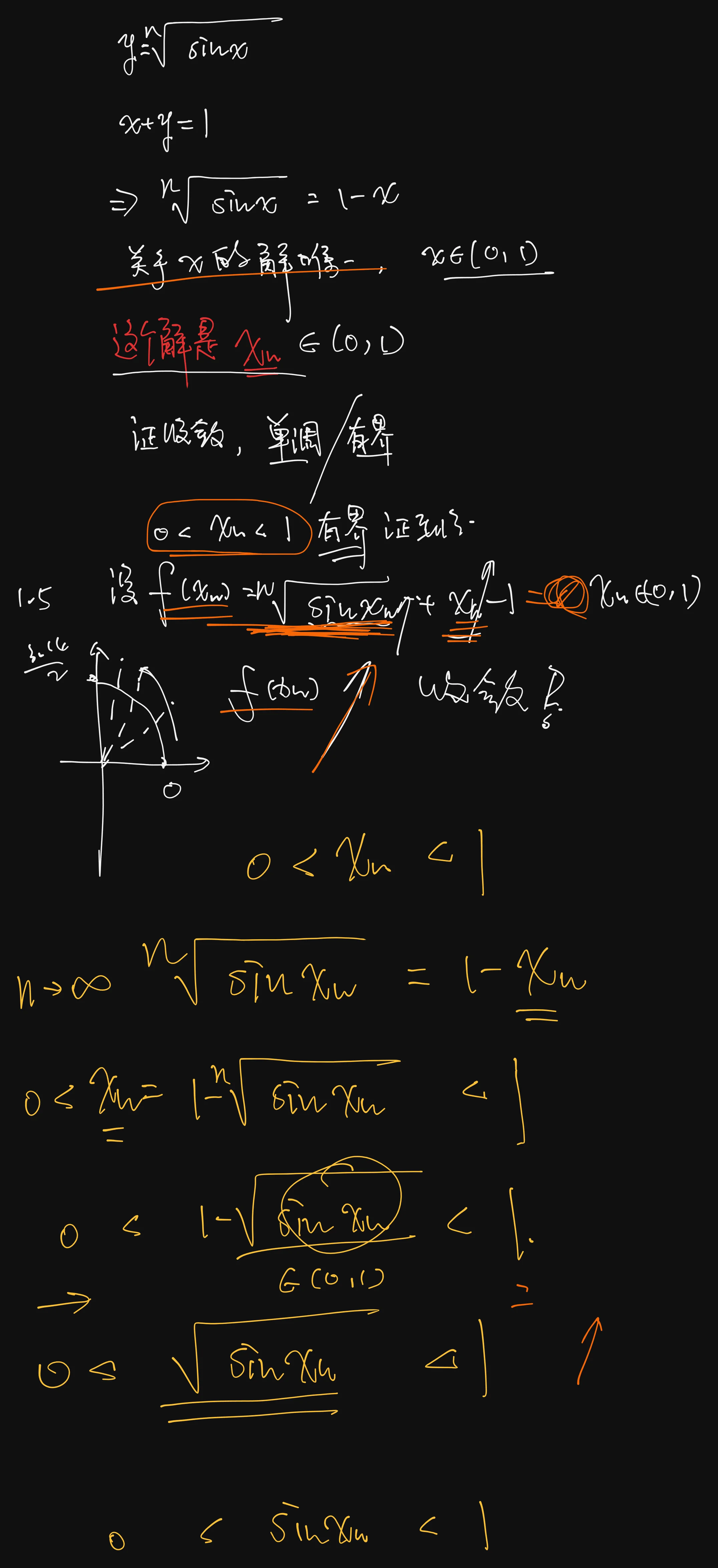例2.27
题目
Q:P83 (1) 证明曲线
(2) 证明 (1) 中的
(3) 计算
分析
A:交点的问题就是解的唯一性的问题,说明两个函数划上等号的解是唯一的
我卡在了,没办法把

这里是用反证法
做错了的核心在于,被绕进去,把数列和函数糅在一起了
还要额外注意,这一句:
即
函数的单调性,可以反过来判断自变量的大小关系
解
(1)【证】令
又
(2)【解】由 (1) 知,
故
即
由单调有界准则,有
当
等式左边为
(3)【解】
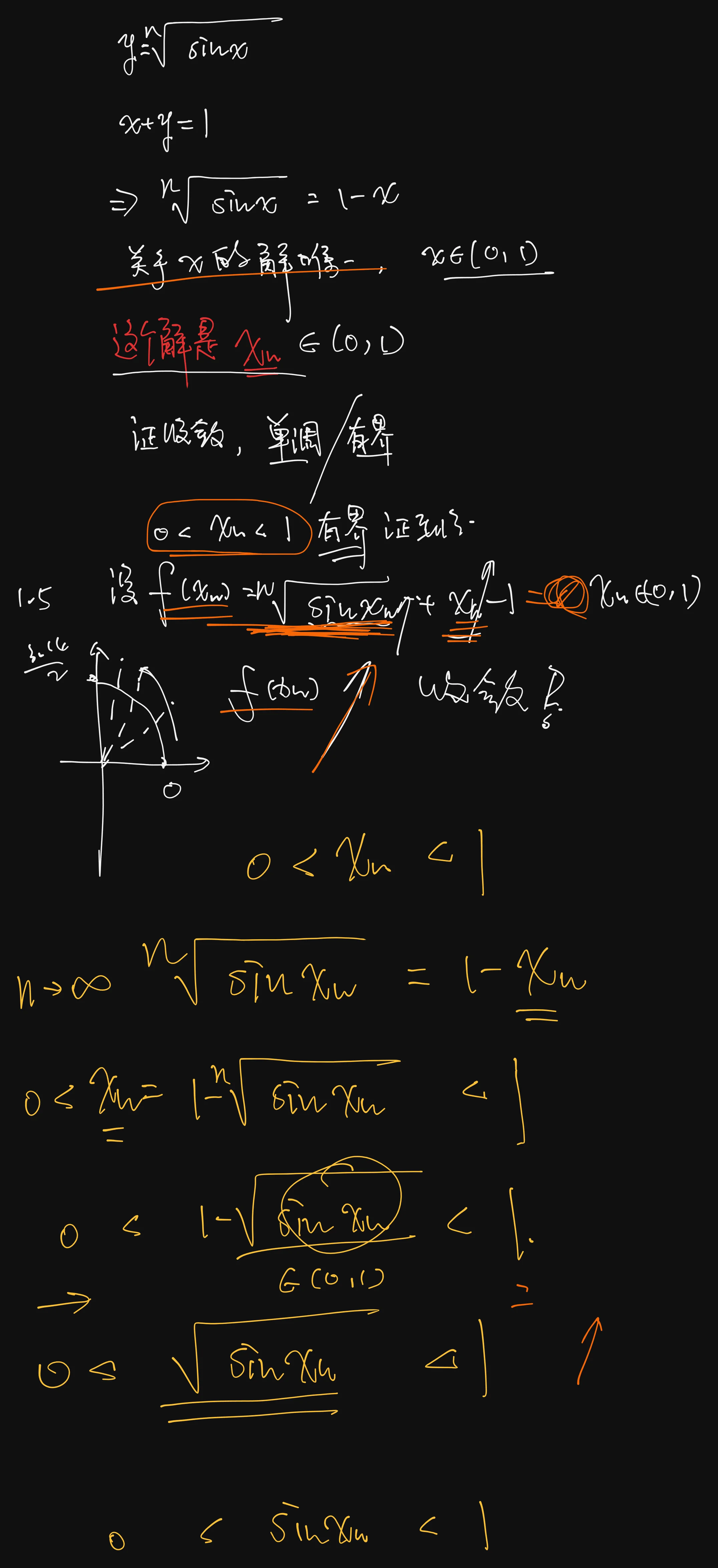
Q:P83 (1) 证明曲线
(2) 证明 (1) 中的
(3) 计算
A:交点的问题就是解的唯一性的问题,说明两个函数划上等号的解是唯一的
我卡在了,没办法把

这里是用反证法
做错了的核心在于,被绕进去,把数列和函数糅在一起了
还要额外注意,这一句:
即
函数的单调性,可以反过来判断自变量的大小关系
(1)【证】令
又
(2)【解】由 (1) 知,
故
即
由单调有界准则,有
当
等式左边为
(3)【解】