例2.20
题目
Q:P79 设数列
分析
A:2023数二原题:题3
数列的后项比前项,极限是0,直接得到极限是0
找
现在在数列这章目前的手段就是
比如找到
这个
或者说,放缩这就要求把不可解的式子,比如这里的
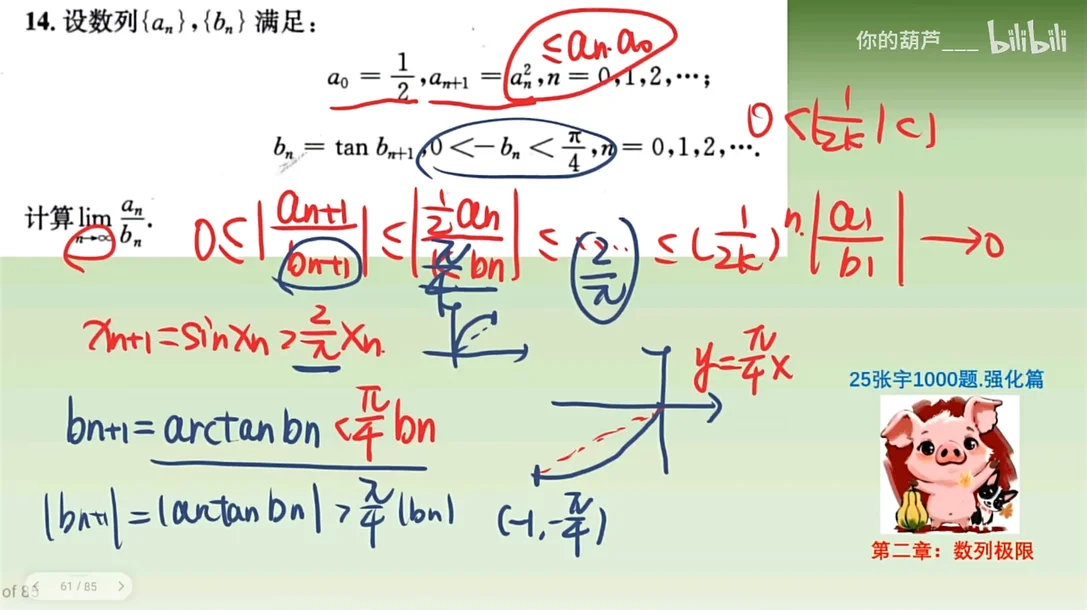
解
令
因此有

Q:这里需要积累一个把sin放缩出来常数k的不等式,邂逅遗憾把这个叫几何放缩
A:也就是

Q:P79 设数列
A:2023数二原题:题3
数列的后项比前项,极限是0,直接得到极限是0
找
现在在数列这章目前的手段就是
比如找到
这个
或者说,放缩这就要求把不可解的式子,比如这里的

令
因此有

Q:这里需要积累一个把sin放缩出来常数k的不等式,邂逅遗憾把这个叫几何放缩
A:也就是
