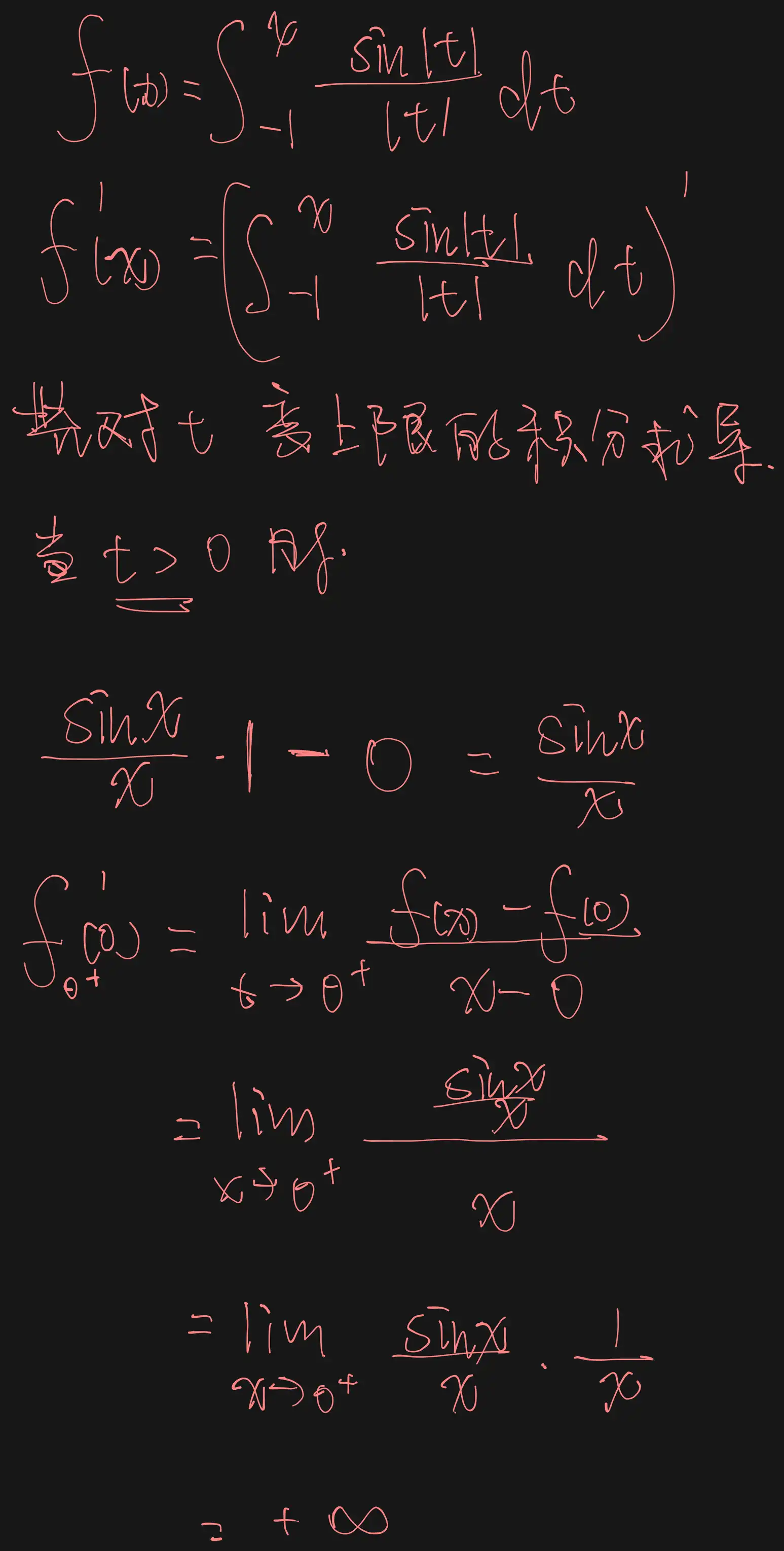例1.13
题目
设 ,则
(A) 不存在且为
(B) 存在且不为零
(C) 存在且为零
(D) 不存在且
分析
首先要想到去用定义
应该先求导,然后从定义的角度来看,和例1.12是类似的,但是这个不是考的变限积分求导公式,而是直接带入这个积分的式子用定义,需要我们自己先尝试这个特殊点,然后算极限
这个带绝对值的函数也是重要的考点,我经常错,对它一些性质认识不够
求某点的导数,要先看存不存在,也就是左右导数是否相等
下面是我当时做错了的记录
05:17 邂逅哥介绍了导数极限定理
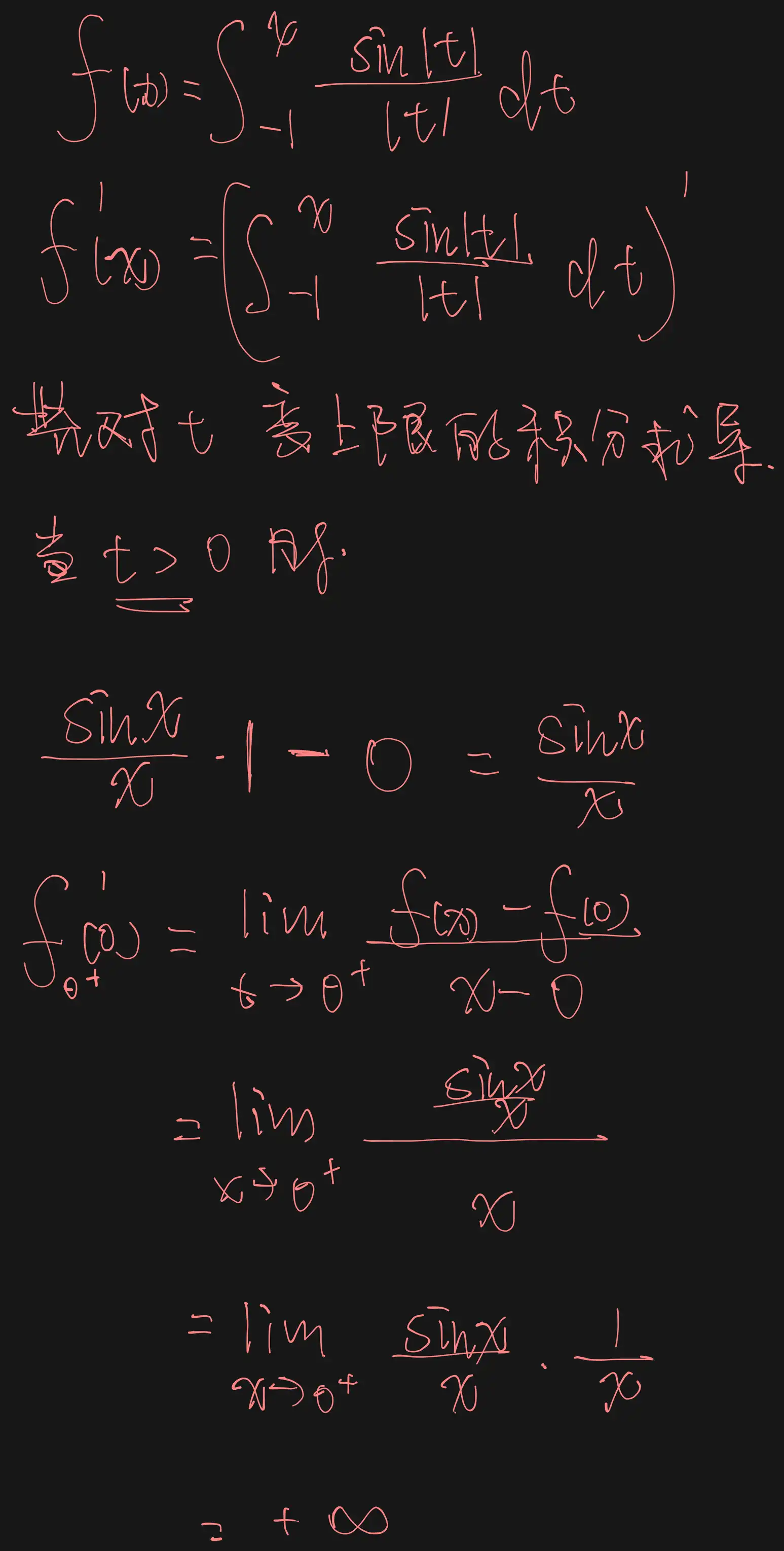
解
下面这又是这个变限积分,和间断点,判断得到说一定可导的那个知识点:由于,故是的可去间断点,可知在处必可导,且